Satellite Line-of-Sight Intersection with Earth
There a fun little real-world problem that many GIS engineers run into that I think demonstrates the elegance of geometry, algebra, imaginary numbers, and vector math. It’s pretty, simple, but it’s fun. The problem is illustrated in the figure below.

This problem comes up frequently with imaging satellites. Suppose you have an image like the one shown below. Our camera has a model that gives us a 3D direction vector for each pixel in the image that points from the satellite to the pixel.

Let’s start with the things that we know. The Earth is a slightly squished sphere (an ellipsoid). The distance from the center of the Earth to the poles is a little less than the distance to the equator. The WGS-84 ellipsoid model of the Earth yields the following dimensions:
- Polar Radius: 6,356,752.314245 meters
- Equatorial Radius: 6,378,137.0 meters
We are also assuming that we know the 3D position of the satellite as a vector (x, y, z) and the direction vector pointing toward the pixel (u, v, w). For shorthand, we’ll call the satellite vector s, the pointing vector û, and the point on the Earth that we are trying to find p.
The “hat” on the point vector û simply denotes that it is a unit-vector. A unit-vector is a vector that has a length of one. It gives you a direction, but not a distance. This is all the information we need to find where the satellite’s line-of-sight intersects Earth! Let’s setup our problem.
Let’s think about how we can relate the satellite’s position, it’s pointing vector, and the the point on the ground. If we start from the satellite’s position, there must be a positive multiple the pointing vector such that it touches the Earth. This is visualized in the figure below.There must be some positive multiple of the the pointing vector such that pointing We can at least say that
s + dû = p
for some positive number d.

The equation of an ellipsoid is

For the WGS-84 geoid, a and b are the equatorial radius. c is the polar radius. Let’s plus in the values for x, y, and z from equation that defined p.

We know, everything in this equation except for d! If we multiply out this equation and simplify we’ll have a quadratic equation as a function of d. Let’s plus in some numbers to make this easier to visualize:
- S = (1e7, 1e7, 1e7) meters
- û = (-0.7274, -0.3637, -0.5819)
- a = b = 6,378,137.0 meters
- c = 6,356,752.314245 meters
The equation then becomes:

Now it’s hopefully a little more obvious that this is a simple quadratic equation for d. Let’s simplify our equation as a function of d. The math gets pretty messy by hand, so let’s use Python to help us out! There’s a great package for Python called SymPy that’s great for math like this. Here’s the code to do it:
The solutions are too long to write out here, but they have the following form:

What’s nice about this is that a, b, and c are just the dimensions of the Earth geoid, so that’s always a positive number. That’s important, because we can now reduce our answer to one solution. We only need the answer with the subtraction. Why? Because, we want the smallest value of d for which the pointing vector û intersects the Earth. So our solution ends up being just

So what’s the other solution? And what happens if the radical is negative and we get an imaginary answer? The solution where we sum the radical stuff is where the vector pops out on the other side of the Earth. Our math doesn’t know anything about the Earth being solid.

And what if the answer if imaginary? The answer will be imaginary if the line of sight misses the Earth as shown below.
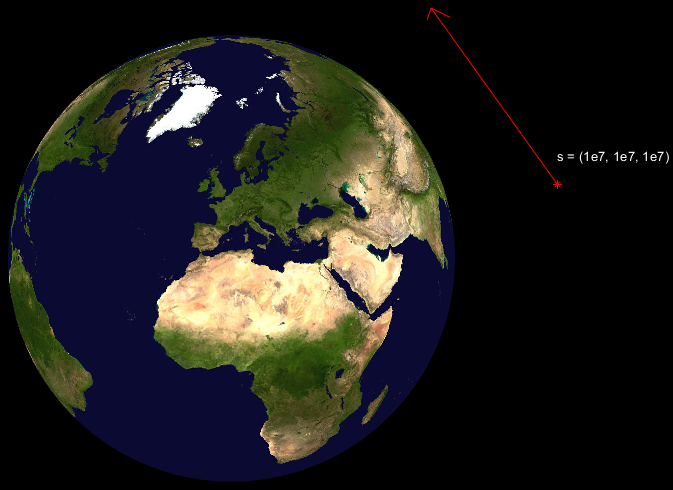
If the radical is exactly zero, then the line-of-sight just barely intersects at the very edge of the Earth in exactly one place. we need to watch out for one other case. What if the solution is negative? The solution will be negative if the line-of-sight is pointing away from the Earth.

Here’s a bit of Python code that puts all this together!
